I love finding ways to measure parts and circuits with my tracking generator + spectrum analyzer (TG + SA).
I show early experiments with a jig developed to derive crystal motional parameters with a TG +SA plying the G3UUR method. Crystal parallel capacitance (C0) is measured separately with an LC meter. My hope is to accurately characterize fundamental crystals in the 20-50 MHz range to make crystal ladder filters for VHF projects.
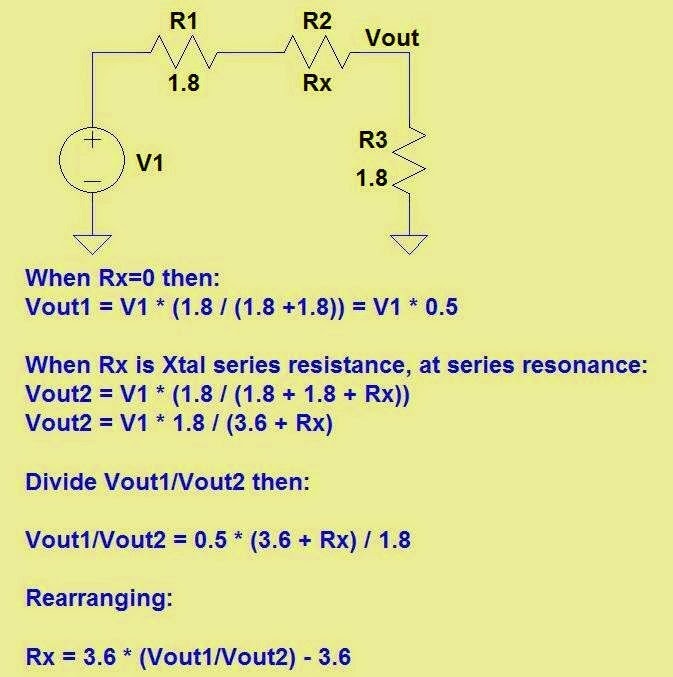
Above — Schematic of the series jig for characterizing xtals with the G3UUR method. Each 50 Ω port gets an impedance drop by a trifilar transformer and L-pad down to 1.811 Ω to help eliminate any xtal parallel capacitance effects during measurement. The L-pad attenuates the signal by ~ 10.1 dB to help establish the crystal input/output Z.
Cs, the series capacitor = a Vishay 1%, Q = 2500 @ 1 MHz, size 0805 C0G capacitor measured at 30.8 pF before going into the circuit. The transformers = 8 trifilar windings on a FT37-43 ferrite toroid.
Above — 2 views of the early breadboard with a 40 MHz crystal in the holder. I shortened and better grounded the 9:1 Z transformers after taking these pictures. Built on double-side Cu board, several Cu via wires pass through to establish a solid ground plane. This helped boost the input + output return loss to get close as possible to the desired crystal 1.811 Ω source and load Z.
The switch = a slide-on shorting switch often employed in computer motherboards.
Measures with a 40 MHz Crystal
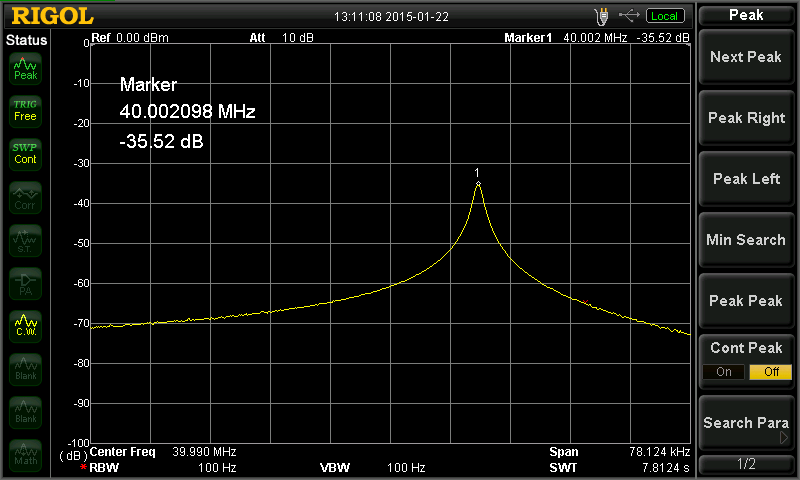
Above — A sweep of the crystal series resonant frequency. I ran the RBW at 100 or 30 Hz but either worked fine — and of course, 100 Hz gives faster sweeps. The series resonant frequency = 40.002098 MHz.
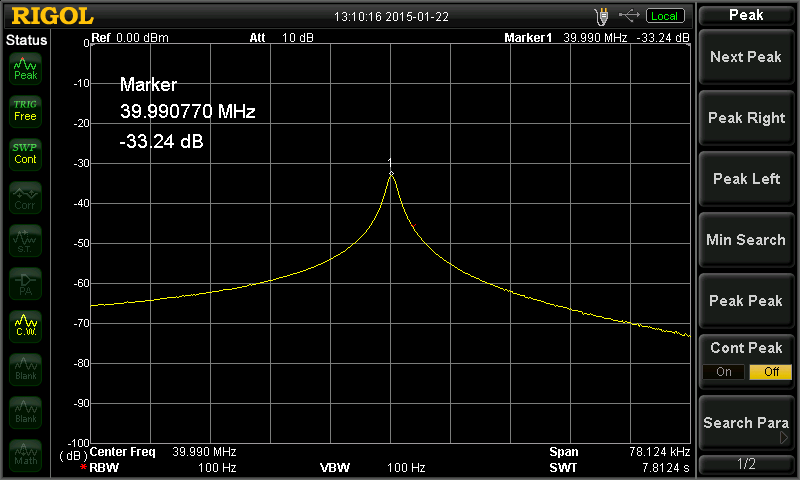
Above — A sweep after adding the Cs switch shorting pin with a gloved hand and allowing time to stabilize before recording frequency and power. F = 39.990770 MHz. Power (referenced to 0 dBm) = -33.24 dBm.
Above — A sweep with the shorting pin still on the switch --- but the crystal removed and replaced with a copper shorting wire stuck into the crystal holder. Through power = -28.39 dBm.
Delta P = the power difference in dB between the series resonant crystal measure and the power recorded with the crystal holder shorted by a Cu wire [both with the 30.8 pF capacitor shorted]. Delta P = 7.13 dB.
Crystal C0 = 2.73 pF as measured with an AADE meter.
Calculations:
Above — Cm is calculated with the standard formula. After --- calculate the capacitive reactance of Cm and insert this X into the formula to calculate Lm. A scientific calculator makes these equations easy to crunch. Typically we would express Cm as 1.99E-14 on a calculator.
At this point, we've calculated crystal Cm, Lm and have enough data to calculate the ESR at the series resonant frequency + the unloaded Q.
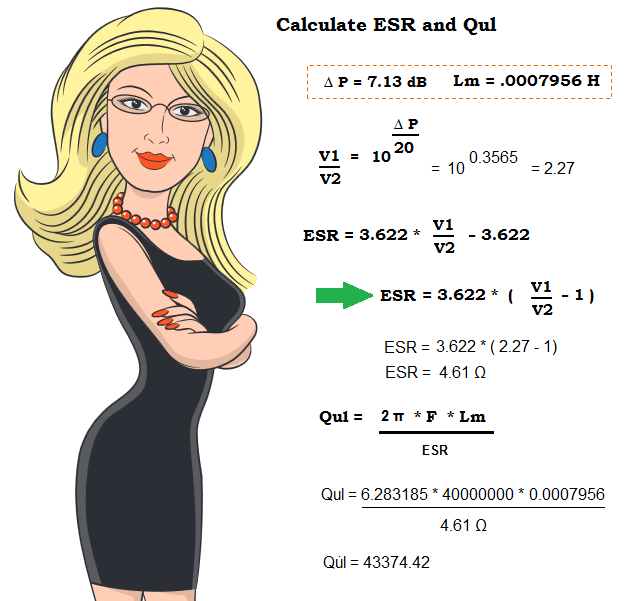
I asked Victor 4Z4ME for help with the calculations for ESR, since once you know the crystal series resistance, Qul may be calculated. Victor sent the below figure that shows how to derive the equation to crunch ESR. Note: 1.8 Ω was used instead of 1.811 for clarity.
Above —Equations to calculate the ESR and Qul. The ESR formula that Victor showed earlier is further simplified to the right of the green arrow [ESR = 3.622 * (V1/V2 - 1) ]. We then use ESR to calculate the unloaded xtal Q as shown.
This 40 MHz job @ 43.4K = a low Q crystal, but it might work OK in a wide IF filter that follows a VHF receiver's first mixer. Most of the crystals >= 30 MHz fundamental I've tested have a Qu < 100K.
Building a collection of fundamental crystal >= 20 MHz proves difficult for me. Several eBay crystal offerings touted to operate on the crystal's fundamental frequency turned out to be overtone crystals. Crystal purchased from vendors like Mouser-Key have better obeyed the their datasheet specification, although, there too, I've found exceptions.
I fundamental frequency test these crystals in an oscillator that outputs to my 50 Ω terminated 'scope.
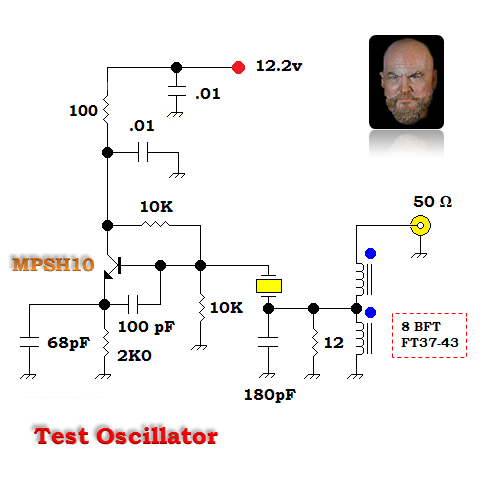
Above — An oscillator I use to test fundamental crystals >= 20 MHz. Although, the BJT listed is a MPSH10, a 2N3904 works OK.
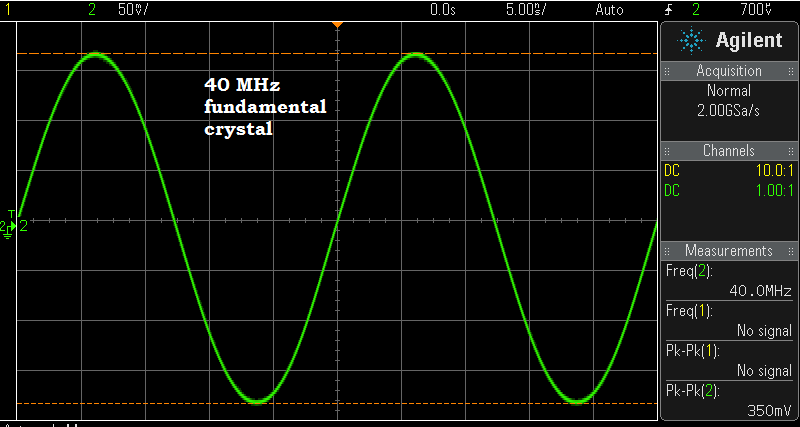
Above — The 40 MHz crystal used for the earlier Cm, Lm, ESR, and Qul calculations vibrating in my crystal test oscillator.
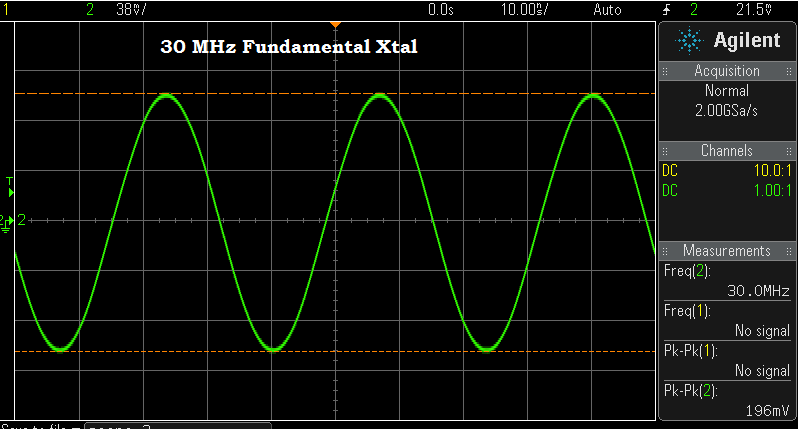
Above — A 30 MHz fundamental crystal in the test oscillator.
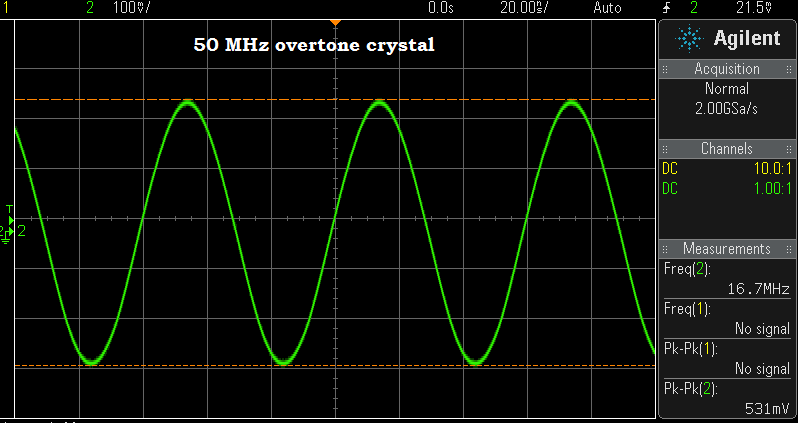
Above — 1 of the many 50 MHz "fundamental" crystals that turned out to be an overtone job.
Conclusion
I measured a 12.0 MHz crystal with the classic G3UUR crystal oscillator method and compared it to the series jig result. The classic xtal oscillator gave an Lm = of 0.0052 H, while the TG + SA series jig gave an Lm of 0.0041 H.
I'm not sure which 1 is correct? Likely the proof of the pudding lies in the transfer functions of the crystal filters I build informed by this new crystal parameter tool.
While it's no panacea, I enjoyed these experiments and learned a lot. For example, I now have 3 methods to measure crystal Q and feel I've advanced a little in my TG + SA skill set
.
My sincere thanks to Wes, W7ZOI for getting me started on this project and also for a few breadboard parts — plus — big thanks to Victor, 4Z4ME for his equations and support.
Best!